
図 1. 3つの生け垣: a <ε> , a <x > , そして a <ε > b < b <ε> x >
MURATA Makoto (村田真)
(試訳・TAKAHASHI Masayoshi (maki@inac.co.jp)
ただし、翻訳の質については、何の保証もありません。 あしからず(_o_))
これは 生け垣オートマトン理論のための予備知識について書いたものです。 XMLコミュニティでは、最近、この理論がXML スキーマのシンプルかつ パワフルなモデルであると思われるようになってきました。 とりわけ、RELAX(REgular LAnguage for XML)の設計では、 この理論が直接の土台となっています。
まず、生け垣(hedge)について説明します。 おおざっぱには、生け垣は木(tree)の並び(sequence)です。 XML用語では、生け垣は文字データ(または文字データの型)を 挟むことのある、要素(elements)の並びです。 とりわけ、XML文書は生け垣そのものです。
有限集合Σ(シンボル(symbol) の集合)と有限集合X(変数(variable)の集合) 上の生け垣 は以下の通りです:
図 1 は 3つの生け垣を表現しています。 それぞれ、
「a <ε>」 「a <x>」 「a<ε>b<b<ε>x>」
です。 Σの要素(すなわち aとb) が葉(leaf)ではないノードのラベルとして使われていて、 Xの要素(すなわち x ) が葉となるノードのラベルに使われているのに気づくでしょう。 a <ε>は aと省略します。 よって、三番目の例は a b <b x > を表しています。

図 1. 3つの生け垣: a <ε> , a <x > , そして a <ε > b < b <ε> x >
次に、XML文書について考えてみます。 Σ = {doc, title, image, para} かつ X ={#PCDATA}とします。 そうすると、
doc < title<#PCDATA> para<#PCDATA> <image/> para<#PCDATA>>
は生け垣になります。XMLの文法では、この生け垣は 以下のように表すことができます:
<doc>
<title>#PCDATA</title>
<para>#PCDATA</para>
<image/>
<para>#PCDATA</para>
</doc>
このセクションでは、 正規生け垣文法(regular hedge grammars) (RHGs)を紹介します。 RHG は 生け垣を生成するためのメカニズムです。 言い換えれば、 RHGは生け垣の集合を表現します。
XML スキーマの第一の役割は validな文書の集合を表現することであるため、 RHGはXML スキーマの形式的表現であると考えることができます。
正規生け垣文法 (RHG)は 5つの要素のタプル、 <Σ, X, N, P,rf >からなります。 各要素の詳細は以下の通りです:
さて、RHGの 導出(derivation) について考えましょう。 おおざっぱに言えば、 非終端記号の並びが与えられたとき、 その非終端記号を、対応する生成ルールの右側にある生け垣に、 繰り返し置き換えていきます。
以下の場合、 生け垣vは生け垣uから直接導出すると言います:
Gから生成される言語 (これはL(G)と書きます)は、 rf にマッチする 非終端記号列から導出される生け垣の集合です。
RHG G = < a, x, {n1, n2}, P, n1?> とします。ここで、Pは、
P = {n1 → a<n2+ >, n2 → x }.
であるとします。
そうすると、
L(G) ={ε, a<x >, a<xx>, a<xxx >, ...}
となります。
つぎに、DTDを真似たRHG を構成してみましょう。 例として、以下のような DTD を考えてみましょう:
<!ELEMENT doc (title, (para|image)*)> <!ELEMENT title (#PCDATA)> <!ELEMENT para (#PCDATA)> <!ELEMENT image EMPTY>
この DTD は以下のようなRHG G = <Σ, X, N, P, nd > で表わすことができます:
つづいて、以下を満たすRHG G = <Σ, X, N, P, n1 > を考えます:
非終端記号n1 に対するルールも n2に対する ルールも、右側にsegment があります。 しかし、前者は np* n2* の内容モデルを持っていて、後者は np*の内容モデルを持っています。 これは、最上位のsegmentは従属するsegmentを持てるが、 従属するsegmentは、さらにその下に属するsegmentを持つことは できないことを意味しています。
DTD文法では、このRHGを正確に表現することができません。 これは、全てのsegmentが同じモデルを持つことしかできないためです。 このRHGをカバーする最小のDTDは以下の通りです:
<!ELEMENT segment (para*, segment*)> <!ELEMENT para (#PCDATA)>
このDTDはsegmentが際限なく入れ子になることを許してしまうのに 気をつけてください。 DTD文法が二つの内容モデルを持つことが許されないため、 このDTDはゆるい内容モデルを一つだけ使っています。
このセクションでは、 決定的生け垣オートマトンと 非決定的生け垣オートマトンを紹介します。
決定的生け垣オートマトン deterministic hedge automaton (DHA) は、以下を満たす < Σ, X, Q, α, ι, F>です:
図2は 図1の生け垣に対してDHAを実行した結果です。
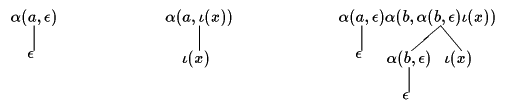
図2. 決定的生け垣オートマトンの実行
次に、正規生け垣文法のセクションでの最初の例を受理するDHAを示します。 M = <a , x , { q0, q1, q2 }, α, ι, q1? }, を以下を満たすものとしましょう:
そうすると、
L(G) ={ε , a<x> , a<xx> , a<xxx> , ... }
次に、非決定的生け垣オートマトンを紹介します。 非決定的生け垣オートマトン non-deterministic hedge automaton (NDHA) とは、以下の条件を満たす < Σ, X, Q, α, ι, F> です:
定義より、DHA は同時にNDHAでもあります。 一つの状態と、その状態のみを持つ一要素の集合とを同一視すればよいのです。 よって、先ほどのDHAはNDHAの例にもなっています。
RHGの章での最後のRHGの例は、 以下を満たす NDHA <Σ, X, Q, α, ι, F > で表現することができます。
以下の条件は等価です。
(3) が (2)を含むことの証明は部分集合構成法によってできます。 残りの証明も容易です。
集合 L1 と L2 が、それぞれ (N)DHA M1 と M2 に受理されると仮定します。 この場合、以下の言語を受理する(N)DHAsを実際に構成することができます。
拡張文脈自由文法の解析木の集合は 局所(local)木言語と言われます。 局所木言語と正規生け垣言語の関係はよく知られています。 ここではXMLに直接関連する二つの知見に触れておきます。
(1)はRHGがDTDよりも表現力が豊かであることを意味しています。また、 (2)は与えられたすべてのRHGについて、適切なDTDが 構成できることを保証します。
In the theoretical computer science community, regular hedge languages were first studied by Pair et al[PQ68] and Takahashi[Tak75]. Regular hedge language can also be considered as extensions of regular tree languages [Tha67]. We borrow some concepts from these papers but adopt definitions more similar to those for regular string languages.
We define RHG's similarily to [PQ68,Tak75], but we avoid projections. Alternatively, our definition can be considered as a hedge-version of Brainerd's tree regular grammars (called "tree generating regular systems) [Bra69].
Our definitions of NDHAs and DHAs are derived from (non-)deterministic tree automata of [Tha67] except that we have extended them to hedges.
It was Kil-Ho Shin (Fuji Xerox) who first proposed to use regular hedge languages as a formal model for schemata of structured documents. His proposal dates back to November, 1991, but he never published any papers. In search of a formalism for document schemata, HIYAMA Masayuki (FAMILY Given) reached a similar formalism in 1996. Since 1993, the present author has applied regular hedge languages (and hedge monoids, which are outside the scope of this note) for schema transformation [Mur97a,Mur97b,Mur98].
The word ``hedge'' was originally proposed by Bruno Courcelle [Cou89]. Derick Wood recommended the use of this word, and it has become the standard word in the XML community after a tutorial by Paul Prescod in 1999. For more information, see the special section on hedge automata in the he SGML/XML Web Page (http://www.oasis-open.org/cover/topics.html#forestAutomata).
[Mur97a] Makoto Murata. DTD transformation by patterns and contextual conditions. In Proceedings of SGML/XML'97 (Also available at http://www.fxis.co.jp/DMS/sgml/xml/sgmlxml97.html and http://www.fxis.co.jp/DMS/sgml/xml/dtd_transformation/index.html) . GCA, 1997.
[Tha87] James W. Thatcher. Tree automata: An informal survey. In Alfred V. Aho, editor, Currents in the theory of computing, pages 143--172. Prentice-Hall, 1987.